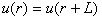Lattice dynamics

In this the final chapter of the thesis perhaps the most interesting results will be presented. Here we will start with a short review of harmonic lattice the-ory together with a brief discussion of how lattice dynamics can be calculated from ab-initio theory. Here special focus will be on the so-called supercell method, since this is the method that has been used through out this thesisto calculate phonons from ab-initio theory. After this brief introduction theresults obtained within the harmonic, or rather quasi harmonic, approxima-tion will be presented (see papers III, IV and VI). The chapter is ends with adiscussion of the anharmonic lattice and a presentation of the self-consistentab-initio lattice dynamical (SCAILD) approach, and the results obtained withthis novel approach (see paper V) will also be discussed.

The Born Oppenheimer approximation

Before discussing the theory of lattice dynamics and the associated calcula-tional methods, it is important to take a closer look at one of the fundamental approximations used in calculating phonons from first principles. This approx-imation is commonly known as the Born Oppenheimer approximation, and itassumes that the electronic response to an atomic displacement is instanta-neous, making it possible to separate the electronic and the ionic subsystems.To convince oneself of the soundness of this approximation one should remember that the typical ionic mass mi is ∼ 105 times bigger than the mass ofan electron me and that the typical kinetic energy of an electron Eke is 103 times bigger than the typical ionic kinetic energy Eki, implying that the ratiobetween the typical velocity of an electron ve and that of an ion vi becomes(ve/vi)=%Ekemi/(Ekime) ∼ 104. Thus from the "perspective of an electron",the ions will always seem to have fixed positions. Hence if U(R) are the de-viations of the ions from their equilibrium positions at a snapshot in time, itis always possible to retain the total energy of the system, at that snapshot,by means of a static electronic structure calculation. Thus, through a seriesof electronic structure calculations, the potential energy of the ionic subsys-tem can be parameterized in terms of ionic deviations. It is general practice toexpress the potential energy in the Hamiltonian of the ionic subsystem, as aTaylor expansion around the equilibrium ionic configuration.

The harmonic lattice

In the harmonic lattice approximation the atomic deviations are assumed to beso small that the potential energy is well described by the second order term in(8.1). This is generally a good approximation, at least at relatively low temper-atures. Later on in this chapter examples of situations will be given in whichthe harmonic approximation fails, such as the high temperature bcc phase ofTi, Zr and Hf. Furthermore, in order to make the notation more transparent,the notation of a monoatomic lattice will be adapted without any loss of gen-erality. The harmonic Hamiltonian in the case of a monoatomic lattice is given by

In the harmonic approximation, the ionic displacements UR satisfy Bornvon Karman periodic boundary conditions. This means that the displacementscan be expressed as a superposition of plane waves with wavevectors k ∈ 1BZ. Hence the canonical coordinates UR and PR appearing in (8.2), can beexpressed in terms of a new set of canonical coordinates Qk,s andPk,s, i.e

The supercell method

In the previous section it was shown that once the force constant matrix has been calculated and Fourier transformed, the phonon frequencies are easilyaccessed by a simple diagonalization. Fortunately there exists a fairly simpleand straightforward method for calculating from first principles, namely theso-called supercell method. The foundation of the method is provided by theHellman-Feynman theorem, stating that the force FR acting on an atom withspatial coordinate R.

From the above linear relation and the symmetry of the crystal the forceconstant matrix can then be easily calculated. The number of displacementsneeded to retain depends on the symmetry of the crystal. For instance inthe case of the bcc or fcc structure one displacement is sufficient, while in thecase of the hcp structure two displacements are needed.However since, at least in principle, Φij(R)→0 only as R→∞, and sinceonly finite sized supercells can be used, the summation in (8.5) has to be trun-cated, and the dynamical matrix can only be approximately calculated. Fur-thermore, due to the periodic boundary conditions employed in the electronicstructure calculations, the linear relation (8.16) is only true if an infinite sizedsupercell is used. In real life all the periodic images of the displaced atomcontribute in the induction of the forces in the supercell. The correct linear re-lation between force and displacement(s), to be used in a supercell calculation.

Some thermodynamics and the quasi harmonic

approximationIn this section relations between the harmonic phonon spectrum and differentthermodynamic quantities, such as the free energy, internal energy and meansquare atomic deviation, will be derived and briefly discussed. Furthermore ashort presentation of the quasi harmonic approximation will also be given.

The two above expressions for the internal- and free-energy have been used inthe context of the so-called quasi harmonic approximation to calculate Equations of state, Hugoniots and thermal expansions (see papers III, IV and VI).What now remains in this section is a short discussion of the quasi harmonic approximation. This is the most simple approximation dealing with theeffects of anharmonicity in which the anharmonicity related to the terms oorder > 2 in the Taylor expansion (8.1) is neglected, only taking into accounthe anharmonicity related to the force constants dependence upon symmetryconserving strain. The simplicity of this approximation lies in the fact thafor each symmetry conserving strain the lattice dynamics of the system isregarded as being harmonic, permitting the use of the supercell method separately for each symmetry conserving strain. In Fig. 8.2 the phonon density ostates for fcc Au calculated with the supercell method for three different volumes are displayed, as an example of the volume dependence of the phonon spectra.

Thermal expansion

In this section the art of calculating thermal expansion coefficients from firstprinciples will be discussed. This discussion will be based on the work donein papers IV and VI of the these.

Thermal expansion of cubic metals

The calculation of the thermal expansion of elements with cubic symmetry isvery straightforward when done in the quasi harmonic approximation. Firstthe phonon and electron density of states together with static lattice energy iscalculated for a number of volumes around the T = 0K equilibrium volume.Then using Eq. (8.28-8.30) the total free energy is calculated for the differentvolumes at constant temperature and fitted to some EOS.

Thermal expansion of hexagonal metals

To calculate the thermal expansion of hexagonal metals, the free energy andstatic lattice energy have to be parameterized with respect to two degrees offreedom. The most general second order parameterization of the free latticeenergy, allowing only symmetry conserving strains, can be expressed with thesix dimensional strain vector ¯ ε =(ε1, ε1, ε3,0,0,0) and the elastic constants.Using this strain vector together with the definitions given in chapter 5, thestatic lattice energy U.

ORLANING COLMENARES

C.I.V.- 18.991.089

BIBLIOGRAFIA:

web.mac.com/petros...2/.../urn_nbn_se_uu_diva-8198-1__fulltext.pdf

---

Connect to the next generation of MSN Messenger  Get it now!

Inelastic neutron scattering and lattice dynamics

Inelastic neutron scattering (INS) is one of the experimental methods to studythe dynamics of materials, the complementary methods being Brillouin spec-troscopy, Raman scattering, infrared spectroscopy and inelastic x-ray scattering.Determination of the crystal structure through diffraction methods gives informa-tion of the atomic positional coordinates i.e. the positions where the inter-atomicpotential has minima. On the other hand, vibrations are related to the shape ofthe potential near these minima. A knowledge of the vibrations gives access to themicroscopic quantities (like inter-atomic interaction potential) involved in thermo-dynamic properties, phase transitions, electronic properties and many others.Collective vibrations (phonons) are the elementary excitations of any orderedsystem in condensed matter. Thermal neutrons, with energies of the order of a fewmeV and de Broglie wavelengths of the order of Angstrom units, are unique probesof these excitations. In principle, a complete determination of the phonon spectrumis possible through inelastic scattering of neutrons. In addition to determination ofthe phonon spectra through experimental methods, an understanding of these spec-tra through theoretical formalisms is essential, for interpretation of the results fromexperiments. Collective vibrations are investigated by means of coherent inelastic neutron scattering. On the other hand, incoherent inelastic neutron scattering ispredominantly employed to study single-particle motions, usually, as has been usedat Trombay, for investigation of materials containing hydrogen for example, ro-tational behaviour of ammonium ions in salts, water in hydrates and dynamics ofvarious subgroups in amino acids. This talk will focus only on experiments andresults from coherent inelastic neutron scattering.In Trombay, apart from certain measurements (for example, to determine thephonon dispersion relation in beryllium) which employed the lter detectorspectrometer (FDS), the triple-axis spectrometer (TAS) has been the instrumentof choice for these experiments, for determination of the phonon density of states(PDOS) or phonon dispersion relation (PDR). The TAS (invented by ProfessorBertram Brockhouse (in 1961) who was honoured with the award of the Nobel Prizein Physics in 1994) is a very important instrument for neutron spectroscopy sinceit allows for a controlled measurement of the scattering function S(Q;E) at anypoint in momentum (Q) and energy (E) space. In TAS, the monochromator singlecrystal (Cu (1 1 1) at Dhruva) determines the energy of the neutron incident onthe sample while the analyzer single crystal (pyrolytic graphite (0 0 0 2) at Dhruva)is used to analyze the spectrum of the neutrons scattered from the sample. Thelaws of momentum and energy conservation governing all scattering experimentsare well-known:

In these equations, the wave vector magnitude k = 2¼, where is the wavelengthof the neutron, and the momentum transferred to the crystal is Q. The subscripti refers to the beam incident on the sample and f to the (nal) beam scattered fromthe sample; G is a reciprocal-lattice vector. The energy transferred to the sampleis hº.At CIRUS reactor, numerous studies of incoherent scattering of neutrons fromhydrogenous materials were carried out; some of them being studies of ammoniumion dynamics in salts, the librational modes of water molecules in single crystalhydrates, amino acids. Most of these studies were carried out using the FDS. Onthe TAS, phonon dispersion relations of materials like magnesium, beryllium, zinc,potassium nitrate, and Sb2S3 were measured. In fact, the determination of thephonon dispersion curves of beryllium were, for the time, largely carriedout on a FDS and gave accurate results, comparable to those obtained on a TASand could extend measurements beyond what were accessible on a TAS. The PDRmeasurements on potassium nitrate (KNO3) were interpreted through latticedynamical computations on the basis of a rigid molecular ion model using theexternal mode formalism the first time that this was done for an ionic-molecular system.

The inelastic neutron scattering and lattice dynamics studies carried out at Dhruva reactor may be broadly classiffed into two categories: studies of geophys-ically important minerals (silicates and carbonates) and those of technologically

relevant materials (high-temperature superconductors, intermetallic superconductors, and ceramics). In the sections that follow, studies carried out on some of these would be described in brief, highlighting the significance of the results.

Geophysically important minerals

With the aim to provide a microscopic understanding of the vibrational and thermo-dynamic properties of geophysically important minerals, studies were carried out on a large number of silicate minerals including the olivine end members forsterite and fayalite, the pyroxene end member enstatite, the garnet mineral almandine,the mineral zircon and the aluminium silicate polymorphs sillimanite, andalusiteand kyanite. Detailed inelastic neutron scattering measurements of the PDR and PDOS supported by group theoretical selection rules and model calculationshave been instrumental in the prediction of the thermodynamic properties of min-erals corresponding to the pressure and temperature at which they are believedto occur in the Earth. All of these minerals have fairly complex structures but acomparatively simple interatomic potential model has been employed to providetheoretical estimates of several microscopic and macroscopic properties includingthe elastic constants, phonon frequencies, dispersion relations, density of states andthermodynamic quantities like specific heat, thermal expansion, equation of stateand melting. Forsterite and enstatite: In forsterite (Mg2SiO4), group theoretical selection ruleswere used as guides for coherent INS experiments on single crystals (carried outat the Brookhaven National Laboratory) to determine the phonon dispersion relations. The model calculations, in fact, reproduced both the phonon frequencies as

well as the neutron intensities (and hence, the polarization vectors) fairly well. Thestructure of forsterite consists of isolated silicate tetrahedra while that of orthoen-statite (Mg2Si2O6) contains chains of these tetrahedra. Measurement of density ofstates were carried out using powder samples at Argonne National Laboratory. INSmeasurements on polycrystalline samples of these minerals show features which area consequence of these structural differences the band gaps found in the phonondensity of states in forsterite are falled by the vibrations of the bridg-ing oxygens in the silicate chains in orthoenstatite. The calculated phonon spectra reproduce these differences. Al2SiO5 polymorphs: Phase transitions amongst the three aluminium silicatepolymorphs sillimanite, andalusite and kyanite have been studied both theoret-ically and experimentally. In the structure of these polymorphs, one aluminium ionis in octahedral coordination and forms edge-sharing chains, the other aluminumion is in tetrahedral coordination in sillimanite, ¯ve-coordinated in andalusite andin octahedral coordination in kyanite. The phonon dispersion curves of the low energy modes of andalusite (figure 1) have been measured on the TASat Dhruva and are complementary to previously reported data (phonon dis-persion curves along [0 0 1]) from measurements at the Paul Scherrer Institute,Switzerland. Measurements on polycrystalline samples of sillimanite and kyanite

Conclusion

This talk has reviewed the extensive work done on various materials (geophysicallyimportant minerals (Al2SiO5 polymorphs, zircon, MnCO3) and technologically im-portant materials (ZrW2O8, °uorohalides, high temperature superconductors)) andthus highlighted the complementary nature of coherent inelastic neutron scatter-ing experiments and lattice dynamical model computations leading to a completeunderstanding of the nature of dynamics of atoms in these materials, and in turn,explaining several data pertaining to macroscopic thermodynamic properties.

ORLANING COLMENARES

C.I.V.- 18.991.089

BIBLIOGRAFIA:

http://www.ias.ac.in/pramana/v63/p73/fulltext.pdf

---

Connect to the next generation of MSN Messenger  Get it now!

Quantum Dynamics of Matter Waves Reveal Exotic Multibody Collisions

At extremely low temperatures atoms can aggregate into so-called Bose Einstein condensates forming coherent laser-like matter waves. Due to interactions between the atoms fundamental quantum dynamics emerge and give rise to periodic collapses and revivals of the matter wave field.
A group of scientists led by Professor Immanuel Bloch (Chair of Experimental Physics at the Ludwig-Maximilians-Universität München (LMU) and Director of the Quantum Many Body Systems Division at the Max Planck Institute of Quantum Optics in Garching) has now succeeded to take a glance 'behind the scenes' of atomic interactions revealing the complex structure of these quantum dynamics. By generating thousands of miniature BECs ordered in an optical lattice the researchers were able to observe a large number of collapse and revival cycles over long periods of time.

The research is published in the journal Nature.

The experimental results imply that the atoms do not only interact pairwise -- as typically assumed -- but also perform exotic collisions involving three, four or more atoms at the same time. On the one hand, these results have fundamental importance for the understanding of quantum many-body systems. On the other hand, they pave the way for the generation of new exotic states of matter, based on such multi-body interactions.

The experiment starts by cooling a dilute cloud of hundreds of thousands of atoms to temperatures close to absolute zero, approximately -273 degrees Celsius. At these temperatures the atoms form a so-called Bose-Einstein condensate (BEC), a quantum phase in which all particles occupy the same quantum state. Now an optical lattice is superimposed on the BEC: This is a kind of artificial crystal made of light with periodically arranged bright and dark areas, generated by the superposition of standing laser light waves from different directions. This lattice can be viewed as an 'egg carton' on which the atoms are distributed. Whereas in a real egg carton each site is either occupied by a single egg or no egg, the number of atoms sitting at each lattice site is determined by the laws of quantum mechanics: Depending on the lattice height (i.e. the intensity of the laser beam) the single lattice sites can be occupied by zero, one, two, three and more atoms at the same time.

The use of those "atom number superposition states" is the key to the novel measurement principle developed by the researchers. The dynamics of an atom number state can be compared to the dynamics of a swinging pendulum. As pendulums of different lengths are characterized by different oscillation frequencies, the same applies to the states of different atom numbers. "However, these frequencies are modified by inter-atomic collisions. If only pairwise interactions between atoms were present, the pendulums representing the individual atom number states would swing synchronously and their oscillation frequencies would be exact multiples of the pendulum frequency for two interacting atoms," Sebastian Will, graduate student at the experiment, explains.

Using a tricky experimental set-up the physicists were able to track the evolution of the different superimposed oscillations over time. Periodically interference patterns became visible and disappeared, again and again. From their intensity and periodicity the physicists found unambiguous evidence that the frequencies are actually not simple multiples of the two-body case. "This really caught us by surprise. We became aware that a more complex mechanism must be at work," Sebastian Will recalls. "Due to their ultralow temperature the atoms occupy the energetically lowest possible quantum state at each lattice site. Nevertheless, Heisenberg's uncertainty principle allows them to make -- so to speak -- a virtual detour via energetically higher lying quantum states during their collision. Practically, this mechanism gives rise to exotic collisions, which involve three, four or more atoms at the same time."

The results reported in this work provide an improved understanding of interactions between microscopic particles. This may not only be of fundamental scientific interest, but find a direct application in the context of ultracold atoms in optical lattices. Owing to exceptional experimental controllability, ultracold atoms in optical lattices can form a "quantum simulator" to model condensed matter systems. Such a quantum simulator is expected to help understand the physics behind superconductivity or quantum magnetism. Furthermore, as each lattice site represents a miniature laboratory for the generation of exotic quantum states, experimental set-ups using optical lattices may turn out to be the most sensitive probes for observing atomic collisions.

Collapse and revival of the matter wave field: The quantum dynamics of Bose-Einstein condensates trapped in an optical lattice reveal exotic multi-body interactions. The image shows a sequence of interference patterns of the atomic samples recorded in steps of 40 microseconds. A single cycle of the dynamics is highlighted (blue-orange). (Credit: Max Planck Institute of Quantum Optics)

ORLANING COLMENARES

C.I.V.- 18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

http://www.sciencedaily.com/releases/2010/05/100514094836.html

---

Connect to the next generation of MSN Messenger  Get it now!

Lattice dynamics and correlated atomic motion from the atomic pair distribution function

INTRODUCTION

The pair distribution function ~PDF! obtained from thepowder x-ray and neutron diffraction experiments has beenshown to be of great value in determining the local atomic structure of materials.1The PDF results from a Fourier trans-form of the powder diffraction spectrum Bragg peaks 1diffuse scattering! into real-space.2For well ordered crystals,apart from technical details, this is similar to fitting theBragg peaks 1 thermal diffuse scattering in the powder pat-tern in a manner first discussed by Warren.3A PDF spectrumconsists of a series of peaks, the positions of which give thedistances of atom pairs in real space. The ideal width of these peaks ~aside from problems of experimental resolution! isdue both to relative thermal atomic motion and to static dis-order. Thus an investigation of the effects of lattice vibra-tions on PDF peak widths is important for at least two rea-sons: first, to establish the degree to which information onphonons and the interatomic potential! can be obtained frompowder diffraction data, and, second, to account for correla-tion effects in order to properly extract information on staticdisorder in a disordered system such as an alloy.

In general, powder diffraction is not considered a favor-able approach for extracting information about phononssince, not only is energy information lost in the measure-ment, but also the diffuse scattering is isotropically averaged.The lattice vibrations are best described from the phonondispersion curves determined using inelastic neutron scatter-ing and high-energy-resolution inelastic x-ray scattering onsingle crystals.4,5Nevertheless, with the advent of high-energy synchrotron x-ray and pulsed-neutron sources andfast computers, it is possible to measure data with unprec-edented statistics and accuracy. The PDF approach has beenshown to yield limited information about lattice vibrations in powders, though the extent of which this information can beextracted remains controversial.7–10Measuring powders has the benefit that the experimentsare straightforward and do not require single crystals. It isthus of great interest to characterize the degree to whichlattice vibrations are reflected in the PDF using simple mod-els, such as the Debye model, in situations where detailedinteratomic potential information is not available. In this pa-per we explore these issues by comparing both measuredPDFs and those calculated from realistic potential modelswith PDFs obtained through a single-parameter Debyemodel. This comparison is carried out as a function of atomicpair separation, temperature and direction in the lattice. Wefind that a single parameter Debye model explains much ofthe observed lattice vibrational effects on PDF peak widths,including the temperature dependence, in crystals like Ni,Ce, and GaAs. However, small but non-negligible deviationsfrom the Debye model calculation are evident in crystalwhich needs a long-range interaction to explain anomalies inthe dispersion curves.

CORRELATED ATOMIC MOTION IN REAL SPACE

The existence of interatomic forces in crystals results inthe motion of atoms being correlated. This is usually treatedtheoretically by transforming the problem to normal coordi-nates, resulting in normal modes ~phonons! that are non-interacting, thus making the problem mathematically tract-ible. Projecting the phonons back into real-space coordinatesyields a picture of the dynamic correlations. This situationcan be understood intuitively in the following way. Figure 1shows a schematic diagram of atomic motion in three differ-ent interatomic force systems, each with its correspondingideal PDF spectrum. In a rigid-body system Fig. 1-a, the

interatomic force is extremely strong and all atoms move inphase. In this case, the peaks in the PDF are delta-functions.At the opposite extreme the atoms are non-interacting ~theEinstein model! and move independently as shown in Fig.1b!. This type of atomic motion results in broad PDF peakswhose widths are given by the root mean-square displace-ment amplitude (A^u2&). In real materials, the interatomicforces depend on atomic pair distances, i. e., they are strongfor nearest-neighbor interactions and get weaker as theatomic pair distances increase. In fact, these interactions areoften quite well described with just nearest-neighbor or first-and second-nearest-neighbor coupling. The case of nearest-neighbor interactions is shown in Fig. 1c!. In this Debye model a single parameter corresponding to the spring con-stant of the nearest-neighbor interaction is used. Here, near-neighbor atoms tend to move in phase with each other, whilefar-neighbors move more independently. As a result, thenear-neighbor PDF peaks are sharper than those of far-neighbor pairs. This behavior was first analyzed by Kaplowand co-workers in a series of papers11–13for a number ofelemental metals.

EXPERIMENTS AND ANALYSIS

The experimental PDFs discussed here were measured us-ing pulsed neutrons and synchrotron x-ray radiation. Theneutron measurements were carried out at the NPD diffrac-tometer at the Manual Lujan, jr., Neutron Scattering Center~LANSCE! at Los Alamos and the x-ray experiments atbeam line A2 at CHESS Cornell!. Powder samples of Niand a polycrystalline Ce rod were loaded into a vanadiumcan for the neutron measurements, carried out at room temperature. Powdered GaAs was placed between thin foils ofkapton tapes for the x-ray measurements, measured at 10 Kusing 60 KeV (l50.206 Å) x rays. Due to the higher x-rayenergy at CHESS and relatively low absorption coefficient ofGaAs, symmetric transmission geometry was used.Both the neutron and x-ray data were corrected14,15forexperimental effects and normalized to obtain the total scat-tering function S(Q), using programs PDFgetN.

DISCUSSION

The mean-square relative displacements sij2and the cor-responding correlation parameter shown in Figs. 2, 4, 5, 8,and 9 present two interesting pieces of information about the atomic motions in a crystalline material. First of all, theyshow that nearest-neighbor atomic motion is significantlycorrelated. Second, the details of the motional correlations asa function of pair distance display structures which deviatefrom the predictions of the simple CD model. Here we canraise some interesting questions. How is this structure in themotional correlation of atom pairs related to the underlyinginteratomic potentials? Can one extract the potential param-eters using an inverse approach to model the PDF peakwidths with the potential parameters as input?Reichardt and Pintschovius8argued that the calculatedPDF peak widths as a function of pair distance are ratherinsensitive to the details of the lattice dynamics models usedto calculate sij2. They found that PDFs calculated using ei-ther very simple or complex models didn't show significantdifferences. A similar conclusion has been reached by Graf etal.,10in contradiction to previous claims by Dimitrov et al.7Indeed, the magnitude of errors implicit in the measurementand data analysis appear to be comparable to the effects thatmust be measured to obtain quantitatively accurate potentialinformation using this approach.9The conclusions of Rei-chardt and Pintschovius and Graf et al. and Thorpe et al. arelargely borne out by the present work; e.g., the grossly over-simplified CD model, which neglects elastic anisotropy andparameterizes the dynamics with a single number u ,is rather successful at explaining the smooth rijdependence ofthe PDF peak widths.Thus, when the BvK force parameters are not available,we have shown that the correlated Debye CD model is areasonable approximation to describe both the smoothrij-dependence and the temperature dependence of sij2insimple elements. Considering the poor correspondence be-tween the Debye phonon density of states and the BvK den-sity of states, the reasonable agreement between the BvKmodel calculations of sij2and that of the CD model is rathersurprising. This confirms that the PDF peak width is ratherinsensitive to the details of the phonon density of states andthe phonon dispersion curves, as suggested by Reichardt andPintschovius and by Graf et al. Any information about theinteratomic forces in the PDF peak widths is contained in thesmall deviations of the sij2from those of the CD model cal-culations. Therefore, extracting interatomic potential infor-mation from the PDF peak widths is unlikely. However,these deviations could possibly yield some average phononinformation. For example, recent calculations by Graf et al.10showed that one can obtain phonon moments within a fewpercent accuracy for most fcc and bcc crystals using thenearest-neighbor force parameters extracted from a theoreti-cal BvK PDF spectrum. This result indicates that the PDFspectrum contains some average phonon information, although it doesn't provide detailed phonon dispersion infor-mation. The average phonon information, such as phononmoments from the PDF peak widths, will be a usefulcomplement to optical and acoustic techniques that yieldzone-center information in situations where single crystalmeasurements are not possible. This complementarity alsoextends to the extraction of Debye-Waller factors from pow-der diffraction measurements.Finally, a comparison of the CD model calculations of the PDF peak widths in GaAs with those of experimental PDFand Kirkwood model calculations shows additional limita-tions of the CD model. In the CD model calculation, thenear-neighbor PDF peaks below r<5>

 

 

 

ORLANING COLMENARES

C.I.V.- 18.991.089

 

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

 

BIBLIOGRAFIA:

http://nirt.pa.msu.edu/papers/03jeongprb.pdf

---

Invite your mail contacts to join your friends list with Windows Live Spaces. It's easy! Try it!

Femtosecond Lattice Dynamics in Photoexcited Bismuth

One of the grand challenges of ultrafast science is to follow directly atomic motion of a photo-induced reaction on the fastest time-scales and the shortest distances—those associated with the atomic vibrations and the making and breaking of the interatomic bonds. This is the regime that ultimately governs chemistry and materials characteristics. X-ray bursts produced from a free electron laser promise to be an ideal probe to meet this challenge because of their atomic-scale structural sensitivity and ultra-short pulse duration, which can "freeze" the atomic motion stroboscopically [1]. However, significant technical advances are needed before these sources can be used to make an atomic movie of the fastest events. In particular, the optical laser pulse used to trigger the reaction in these classes of experiments must be precisely timed with the x-ray pulses that are used to take atomic "snap-shots".

Using the ultra-short x-ray pulses of the Sub-Picosecond Pulse Source (SPPS) and a novel timing method, we observed the femtosecond response of a bismuth solid following intense photoexcitation of charge carriers. Our results provide insight into the fundamental interaction between the electronic states and the microscopic atomic arrangements of the solid. Furthermore, we demonstrated the ability to synchronize an optical laser to a linear accelerator based x-ray source with femtosecond accuracy. Bismuth is a material that shows very strong coupling between electronic and ionic structure. It is a model system that demonstrates a rich variety of ultrafast dynamics in the limit of high density excitations, such as extremely large phonon amplitudes, electronic softening and phase transitions. Using time-resolved x-ray diffraction techniques, we monitored the atomic positions within the bismuth unit cell as a function of time in response to impulsive photoexcitation of carriers (Figure 1). Coherent lattice oscillations were observed similar to those previously seen in a pioneering laser plasma based x-ray diffraction experiment [2]. However, the comparatively large x-ray fluence of the SPPS

resulted in a significant improvement in data quality as well as enabled carrier density dependent studies. We were able to quantify the oscillation frequency and the lattice coordinate the oscillations are occurring about from the time-resolved data. With this information we extrapolated the curvature and minima positions of the double well interatomic potential of bismuth as a function of photoexcited carrier density. Our results were compared to previous density functional calculations of the photoexcited system and are in agreement [3]. Electro-optic sampling methods were used to time the excitation laser pulse with the x-ray probe pulse [4]. In this technique, the electric field of the electron bunch that generated x-rays at the SPPS is used to alter the optical properties of an electro-optic crystal (Figure 2). This alteration is probed with a portion of the optical laser that is used to photoexcite the bismuth sample in crossed-beam geometry. Only the portion of the laser that is propagating within the electro-optic crystal when the electric filed is present will be altered. In this manner, the arrival time of the electron bunch is encoded onto spatial profile of the optical laser. The centroid of the electro-optic feature is used to time stamp each x-ray pulse and the data is compiled accordingly.

These measurements have furthered our understanding of bismuth dynamics far from equilibrium. Our experiments provide the first quantitative characterization of the curvature and quasi-equilibrium position of the interatomic potential of a solid close to a free-carrier induced phase transition. From this, we showed that the electronic softening of the potential is the primary factor determining the frequency of the lattice vibrations. The experiments also demonstrate the successful implementation of an electro-optic timing diagnostic. This technical advancement enabled us to perform femtosecond resolution experiments at a linear accelerator based x-ray source. The experiments were carried out by a collaborative team from 20 different institutions. Portions of this research were supported by the U.S. Department of Energy, Office of Basic Energy Science through direct support for the SPPS and the SSRL. Additional support was received by the Swedish Research Council for Science, the Irish Research Council for Science, the Keck Foundation, the Deutsche Forschungsgemeinschaft, the European Union RTN FLASH, the Austrian Academy of Science, the Stanford PULSE center and the NSF FOCUS frontier center.

ORLANING COLMENARES

C.I.V.- 18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

http://ssrl.slac.stanford.edu/research/highlights_archive/spps07.pdf

---

Connect to the next generation of MSN Messenger  Get it now!

Investigation of lattice dynamics

  

Ab initio investigation of lattice dynamics of fluoride scheelite

Abstract

We report on the phonon dynamics of LiYF4 obtained by direct method using first principle calculations. The agreement between experimental and calculated modes is satisfactory. An inversion between two Raman active modes is noticed compared to inelastic neutron scattering and Raman measurements. The atomic displacements corresponding to these modes are discussed. Multiple inversions between Raman and infrared active groups are present above 360 cm-1. The total and partial phonon density of state is also calculated and analyzed.

Introduction

Researches on YLiF4 crystals are strongly linked to laser technology. The first structural data obtained by Thomas et al. date from 1961[1], just one year after the demonstration of the first laser. At ambient pressure, the crystal cell of YLiF4 is tetragonal with space group I41/a (C4h6). This phase is commonly named the scheelite structure in reference of the CaWO4 crystal. Lithium ions (Li+) are in the center of tetrahedrons composed by 4 fluoride ions (F-). Yttrium ions (Y3+) are in the center of polyhedrons composed by 8 F-. Y3+ can be substituted by rare earth presenting an oxidation state of +3, such as Erbium (Er+3) [2] or Thulium (Tm+3) [3], providing good matrix for upconversion laser. The efficiency of this kind of laser relies on intraionic and interionic process of relaxation that strongly depends on the host matrix[4].

This relationship is evidenced particularly by the multiphonon relaxation process implying electron-phonon coupling[5]. Consequently, a fair knowledge of the structural and dynamics properties of the host matrix is crucial for the development of host matrix. To this end many studies have been carried out on the subject. Phonon frequencies were measured by Raman and IR spectra [6][7][8][9][10]. These methods give information at the center of the Brillouin zone. Inelastic neutron scattering measurement is needed to obtain the complete phonon dispersion curves that are essential to a good understanding of the global vibrational and relevant properties. This was done for LiYF4 by Salaün et al.[11]. Besides experimental work, numerical methods have been developed. Among them we can notice empirical methods, such as rigid ion model (RIM). Using this method, Salaün et al[11] and Sen et al.[12] performed lattice dynamical calculations on LiYF4 providing a large number of interesting results about lattice vibration. Obviously, the correctness and precision of this model is limited by the empirical parameters. Density functional theory is an empirical free parameter methods whose usefulness and predictive ability in different fields[13][14] are known since a long time. Recently, the association of DFT with different techniques such as linear response method[15][16] or direct methods[17][18][19] allows to evaluate phonon dispersion curves without empirical parameter. In particular Parlinsky et al.[20][21] developed a direct method where the force constant matrices are calculated via the Hellmann-Feynman theorem in total energy calculations.

In this work we present a first principle investigation of YLiF4 in its scheelite phase. DFT associated with projector augmented wave (PAW) and direct method were used. Cell parameters, phonon dispersion curve, phonon density of state are discussed and compared with previous experimental or numerical results. To our knowledge, this is the first ab initio calculation of LiYF4 lattice dynamics.

Methodology

Cell parameter and atomic positions of the initial structure were obtained from experimental results by E. Garcia and R.R Ryan[22]. All calculations were carried out with the VASP[23] code, based on DFT [24][25], as implemented within MEDEA[26] interface. Here the generalized gradient approximation (GGA) through the Perdew Wang 91 (PW91)[27] functional and projector augmented wave (PAW)[28] were employed for all calculations. Electronic occupancies were determined according to a Methfessel-Paxton scheme[29] with an energy smearing of 0.2 eV. The crystal structure was optimized without the constraints of the space group symmetry at 0 Gpa until the maximum force acting on each atom dropped below 0.002 eV/Å. The self consistent field (SCF) convergence criterion was set at 10-6 eV. High precision calculations, as defined in VASP terminology, were performed with a basis set of plane wave truncated at a kinetic energy of 700eV. The Pulay stress[30] obtained on the unit cell was -4 MPa and the convergence of the total energy was within 0.4 meV/atom compared to an energy of 750 eV. Brillouin zone integrations were performed by using a 3X3X3 k-points Monkorst-Pack[31] grid leading to a convergence of the total energy within 0.1 meV/cell compared to a 7x7x3 k-point mesh. PHONON code[19], based on the harmonic approximation, as implemented within MEDEA[26] was used to calculate the phonon dispersion. From the optimized crystal structure, a 2X2X1 supercell consisting of 96 atoms, was generated from the conventional cell to account for an interaction range of about 10 Å. The asymmetric atoms were displaced by +/- 0.03 Å leading to 14 new structures. The dynamical matrix was obtained from the forces calculated via the Hellmann-Feynman theorem. G point and medium precision, as defined in VASP terminology, were used for theses calculations. The error on the force can perturb the translation-rotational invariance condition. Consequently, this condition has to be enforced. A strength of enforcement of the translational invariance condition was fixed at 0.1 during the derivation of all force constants. The longitudinal optical (LO) and transversal optical mode (TO) splitting was not investigated in this work. Consequently, only TO modes at the G point were obtained.

Results and discussion:

Structural parameters.

Shows calculated and previous experimental or numerical structural properties of LiYF4. Compared to the most recent experimental data[32][33] our calculated volume is over-estimated. Nevertheless, the c/a axial ratio, whose evolution is significant in pressure induced transition phase, is close to experimental results. DFT results are strongly dependent on the approximation of the exchange correlation term. It's known that local density approximation (LDA) favorizes high electron densities resulting in short bonds prediction and so in low equilibrium volume. Results obtained by Li et al.[35] and Ching et al. [36] owing to LDA illustrate this behavior. GGA corrects and sometimes over-corrects the failures of the LDA. That's why cell parameters obtained using PW91 differ from experimental results. At least two reasons explain why our results are at variance with Li et al.[35]. The first one is due to the utilization of different parameters such as the energy cut off. The other one can be attributed to the difference of method to evaluate the equilibrium volume. Indeed, during a structure optimization the convergence criterion is set on the stress.

Lattice dynamic.

The phonon dispersion curves along several lines of high symmetry for LiYF4 structure at zero pressure are shown in Figure 1. To evaluate our calculated phonon dispersion curves, the acoustic branches will be first compared to results extracted from ultrasonic measurements and rigid ion models (RIM). Then the modes at the G point will be compared to experimental results obtained from Raman, IR or neutron scattering and RIM. Velocities of sound following different directions of propagation have been evaluated from the slopes of acoustic branches. Our results and experimental ultrasonic velocities at 4.2 K are presented in Table 3. The difference between calculated and measured velocities lies within 5% for 7 velocities out of 8. The 9% of discrepancy is obtained for the acoustic branch following the [001] direction. In this direction the longitudinal acoustic branches are non-degenerate although the modes at the Z point are degenerate. This behavior has been observed on the two phonon dispersion curves calculated with RIM but seems absent from neutron scattering experiments. Concerning the phonon modes, the spectrum contains 36 phonons modes at the G point as expected from the number of atoms per primitive cell.

Conclusion

This work presents at our knowledge, the first ab initio lattice dynamics calculation of fluoride scheelite. Concerning the phonon dispersion curves, satisfactory agreement with inelastic neutron scattering measurement was obtained. Discrepancies between sound velocities calculated from acoustic branches and ultrasonic measurement do not exceed 300m.s-1. Moreover, at the center of the Brillouin zone the error on Raman active modes calculated compared to experimental results does not exceed 9%, the most important error being 33 cm-1. One inversion between the last Bg mode and the fourth Eg mode was put in evidence in comparison with experimental results. Concerning infrared active modes error lies within 8%, the most important error being 25 cm-1. Below 360 cm-1, only one inversion can be notice compared to experimental results, which is less than in RIM calculations. Important differences between ab initio and RIM calculated DOS were put in evidence mainly above 500 cm-1.

ORLANING COLMENARES

C.I.V.- 18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

http://hal.archives-ouvertes.fr/docs/00/02/99/96/PDF/article2.pdf

---

Get news, entertainment and everything you care about at Live.com. Check it out!

Specific Heat Capacities (Continuacion) ... Debye theory

Historical

(a) Classical
Dulong and Petit (1819)
Cv=3Nk, Correct at high temperature

(b) Einstein
Based on Planck's quantum hypothesis (1901)
Quantised energy, Showed exponential dependence of Cv

(c) Debye
Showed complete dependence (1912)

Debye Model

In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat (heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to the Einstein model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low temperature dependence of the heat capacity, which is proportional to T3 – the Debye T3 law. Just like the Einstein model, it also recovers the Dulong-Petit law at high temperatures. But due to simplifying assumptions, its accuracy suffers at intermediate temperatures.

· Uses wide spectrum of frequencies to describe the complicated pattern of lattice vibrations. [It is assumed that hypothetical oscillators generate simple sine waves throughout the crystal and these will displace the atoms away from their equilibrium positions by an amount equal to the amplitude of the sine wave at that point. If we have a whole set of such oscillators generating sine waves of certain frequencies and amplitudes then we might hope that the superposition of such waves will simulate the complicated pattern of the actual atomic vibrations.]
· Assume that the distribution of oscillators is quasi-continuous in w, and so we may use integration instead of summation. [This could not be done in the derivation of the mean energy of a single oscillator where the individual quantum steps might be large compared to kT.]
· Each frequency (mode) contributes an Einstein-like term to C.

The Debye model is a solid-state equivalent of Planck's law of black body radiation, where one treats electromagnetic radiation as a gas of photons in a box. The Debye model treats atomic vibrations as phonons in a box (the box being the solid). Most of the calculation steps are identical.
Consider a cube of side L. From the particle in a box article, the resonating modes of the sonic disturbances inside the box (considering for now only those aligned with one axis) have wavelengths given by

In order to go further there are two problems to solve:
· A density of states function is required
· Need to set the range of frequencies over which the integration is to be performed, i.e. the cut-off or limiting frequency needs to be determined
Neglecting the zero point energy, the mean thermal energy will be given by

for each frequency. The Debye specific heat will take the form,

Debye temperature table

Even though the Debye model is not completely correct, it gives a good approximation for the low temperature heat capacity of insulating, crystalline solids where other contributions (such as highly mobile conduction electrons) are negligible. For metals, the electron contribution to the heat is proportional to T, which at low temperatures dominates the Debye T3 result for lattice vibrations. In this case, the Debye model can only be said to approximate the lattice contribution to the specific heat.

Debye's Contribution to Specific Heat Theory

Einstein's oscillator treatment of specific heat gave qualitative agreement with experiment and gave the correct high temperature limit (the Law of Dulong and Petit). The quantitative fit to experiment was improved by Debye's recognition that there was a maximum number of modes of vibration in a solid. He pictured the vibrations as standing wave modes in the crystal, similar to the electromagnetic modes in a cavity which successfully explained blackbody radiation. The density of states for these modes, which are called "phonons", is of the same form as the photon density of states in a cavity.
To impose a finite limit on the number of modes in the solid, Debye used a maximum allowed phonon frequency now called the Debye frequency uD.

ORLANING COLMENARES

C.I.V.- 18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

http://en.wikipedia.org/wiki/Debye_model

http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/debye.html

www.plato.ul.ie/academic/Vincent.Casey/PH4607SS1/LatticeDynamics.doc

---

Discover the new Windows Vista Learn more!

Specific Heat Capacities

Historical

(a) Classical
Dulong and Petit (1819)
Cv=3Nk, Correct at high temperature

(b) Einstein
Based on Planck's quantum hypothesis (1901)
Quantised energy, Showed exponential dependence of Cv

(c) Debye
Showed complete dependence (1912)

Classical Model

The classical model for specific heats considered the atoms as being simple harmonic oscillators vibrating about a mean position in the lattice. Each atom could be simulated by three simple harmonic oscillators (SHOs) vibrating in mutually perpendicular directions.
For a classical SHO:

Average kinetic energy = ½ kT
Average potential energy = ½ kT
Total average energy per oscillator = kT
Total average energy per atom = 3kT
For N atoms the total average energy = U = 3NkT
The specific heat capacity is

Cv=3*R

Classical treatment - Dulong and Petit - the specific heat capacity of a given number of atoms of a given solid is independent of T and is the same for all solids.

Einstein Model

So far, the treatment of the vibrational behaviour of materials has been entirely classical. For a harmonic solid, the vibrational excitations are the collective, independent normal modes, having frequencies w determined by the dispersion relationship w(k) with the allowed values of k set by the boundary conditions. In the classical limit, the energy of a given mode with frequency w, determined by the wave amplitude, can take any value.
· MB energy distribution: as T is raised F(Ehigh) increases!
· The energy of the atomic vibrations becomes greater as we go from low to high T

Einstein produced a theory of heat capacity based upon Planck's quantum hypothesis. He assumed that each atom of the solid vibrates about its equilibrium position with an angular frequency w. Each atom has the same frequency and vibrates independently of other atoms. The quantum mechanical result, treating each normal mode as an independent harmonic oscillator with frequency w, is that the energy is quantised and can only take values characterised by the quantum number n(k,p) for a particular branch p. A vibrational state of the whole crystal is thus specified by giving the excitation numbers n(k,p) for each of the 3N normal modes. Instead of describing the vibrational state of a crystal in terms of this number, it is more convenient and convenntional to say, equivalently, that there are n(k,p) phonons (i.e. particle like entities representing the quantised elastic waves).

· Einstein replaced the classical SHO with a Quantum SHO: energy does not increase continuously but in discrete steps: 1D SHO,

n=0,1,2…..

· Note that the quantum mechanical expression for the energy implies that the vibrational energy of a solid is non zero even when there are no phonons present: the residual energy of a given mode, 0.5*h*w , is the zero point energy
· choose zero energy at 0.5 h * w
· take
The probability of occupation of this level is:

The total energy of the solid becomes,

Taking account of the zero point energy and using the above result, the mean energy is therefore,

This energy may be considered either as the time-averaged energy for a particular atom, or it can be thought of as the average energy of all the atoms in the assembly at any instant in time.

Einstein model conlusion!

· successfully predicts that C falls with decreasing T
· however, exponential decrease is not observed; if low frequencies are present, then will be small, much smaller than kT even at low temperatures; C will remain at 3kT to much lower frequencies and the fall off is not as dramatic as predicted by the Einstein model
· assumption of 'an average' single frequency w is too simplistic
· need a spread of frequencies - a frequency spectrum!

ORLANING COLMENARES

C.I.V.- 18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

www.plato.ul.ie/academic/Vincent.Casey/PH4607SS1/LatticeDynamics.doc

xbeams.chem.yale.edu/~batista/vaa/node28.html

---

Discover the new Windows Vista Learn more!

General Form

General Form of the Density of States

The diagram below shows a portion of two adjacent surfaces of constant frequency corresponding to frequencies w and w+dw. Owing to dispersion these surfaces are not normal to the direction of the wavevector k. Consider a small pill box bounded by the surfaces w and w+dw centred around the point k. The unit vector normal to the frequency surfaces is n. The pill box has area dS n.
The number of allowed values of k for which the phonon frequency is between w and w+dw is

= Volume of k space/volume occupied by one state (mode)

The integral is extended over the volume of the shell in k space bounded by the two

Surfaces of equal w in k space.

surfaces on which the phonon frequency is constant, one surface on which the frequency is w and the other on which the frequency is w+dw. This is straight forward where k is small, i.e. no dispersion, since the constant frequency surfaces will be spherical. However, for the general situation where k may be large, one has to deal with a much more complicated shape. The problem for us is to evaluate the volume between these surfaces. Owing to dispersion these surfaces are not normal to the direction of the wave vector k.

ORLANING COLMENARES

C.I.V.- 18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

www.plato.ul.ie/academic/Vincent.Casey/PH4607SS1/LatticeDynamics.doc

---

Explore the seven wonders of the world Learn more!

Vibrations, Linear 1D Lattice

Vibrations of periodic systems

The presence of translational periodicity has a profound effect on the vibrational behaviour when the wavelength of the vibrational excitations becomes comparable to the periodic repeat distance, a. For l>>a, however, the behaviour characteristic of an elastic continuum is recovered.
For a periodic array of atoms of length L, periodic (or Born-von Karman) boundary conditions are appropriate, i.e.

Such a boundary condition can be envisged as follows. In the case of a linear chain of N particles, where the nearest neighbours are connected by springs (representing bonds between atoms), with equilibrium spacing a, periodic boundary conditions are achieved by connecting one end of the chain to the other to form a ring of length L=Na, Figure 4a. An integral number of wavelengths must fit into the length L, resulting in allowed K-values for running-wave (travelling wave) states:

An equivalent and more realistic way of understanding periodic boundary conditions involves the imposition of a mechanical constraint forcing atom N to interact with atom 1 via a massless, rigid rod and a spring, Figure 4b.
In contrast to the case for fixed boundary conditions leading to stationary waves, both positive and negative integers are allowed for running wave solutions, and moreover the spacing between allowed k-values is Dkr=2p/L, twice that for standing wave states. Therefore, the number of k-values, corresponding to running wave states, contained in unit volume of k-space is now

The number of distinct states, for a given polarisation type i, having wavevectors between k and k + dk is this density multiplied by the volume of an entire spherical shell in k-space (since both positive and negative k-values are allowed)

A linear chain connected to form a ring of length L=8a. For modes of the form us ~exp (iska), periodic boundary conditions lead to eight modes (one per atom) with k=0, ±2pi/L, ±4pi/L, ±6pi/L, ±8pi/L.

Linear 1D Lattice

· All atoms identical (mass m)
· Lattice spacing 'a'

For small vibrations, the force on any one atom is proportional to its displacement relative to all the other atoms.

Choose atom s

· p takes on both positive and negative values
· c is the force constant and depends on p, i.e. is large for p=1, smaller for p=2, etc..

The displacement for k' is therefore the same as for k. k' consists of a wave of smaller wavelength than that corresponding to k, passing through all the atoms, but containing more oscillations than needed for the description.
We can describe the displacement of the atoms in these vibrations most easily by looking at the limiting cases k = 0 and k = p/a.
· the situation at k = 0 corresponds to an infinite wavelength; this means that all of the atoms of the lattice are displaced in the same direction from their rest position by the same displacement magnitude. For long wavelength vibrations neighbouring atoms are displaced by the same amount in the same direction. Since the long-wavelength longitudinal vibrations correspond to sound waves in the crystal, all of these vibrations with a similarly shaped dispersion curve, whether transverse or longitudinal vibrations are involved, are called acoustical branches of the vibration spectrum. [When k @ 0, dw/dk = w/k = velocity of sound]

In addition to longitudinal vibrations, the linear lattice supports transverse displacements leading to two independent sets (in mutually perpendicular planes) of vibrations that can propagate along the lattice. The forces acting in a transverse displacement are weaker

Longitudinal and transverse modes for a monatomic lattice

than those in a longitudinal one. They give rise to a new branch of dispersive modes lying below the longitudinal branch.

www.plato.ul.ie/academic/Vincent.Casey/PH4607SS1/LatticeDynamics.doc

---

Explore the seven wonders of the world Learn more!

Lattice Dynamics and Specific Heats

Introduction

The static lattice model which is only concerned with the average positions of atoms and neglects their motions can explain a large number of material features such as:

· Chemical properties;

· Material hardness;

· Shapes of crystals;

· Optical properties;

· Bragg scattering of R-ray, electron and neutron beams;

· Electronics structure as well as electrical properties.

There are, however, a number of properties that cannot be explained by a static model. These include:

· Thermal properties such as heat capacity;

· Effects of temperature on the lattice, e.g. thermal expansion;

· The existence of phase transitions, including melting;

· Transport properties, e.g. thermal conductivity, sound propagation;

· The existence of fluctuations, e.g. the temperature factor;

· Certain electrical properties, e.g. superconductivity;

· Dielectric phenomenon at low frequencies;

· Interaction of radiation with matter, e.g. light and thermal neutrons.

Are the atomic motions that are revealed by these factors random, or can we find a good description for the dynamics of the crystal lattice? The answer is that the motions are not random but are constrained and determined by the forces that atoms exert on each other.

Vibrations in solids.

We will examine the vibrational behaviour of atoms in solids. The vibrations are thermally activated with a characteristic activation energy kBT.
Vibrational excitations are collective modes: all atoms in the material take part in the vibrational mode. The influence of translational periodicity characteristics of the structure of crystals has a dramatic effect on the vibrational behaviour when the wavelength of the vibrations becomes comparable to the size of the unit cell. When the vibration wavelength is much larger than the structural variation of the material, the solid may be considered as an elastic continuum (continuum approximation).

Representation

How can we visualise a vibration wave travelling through a crystal, where the space that vibrates is not continuous (like a string on a musical instrument) but is composed of discrete atoms? The answer is to think of the wave as representing displacements, u(x,t), of the atoms from their equilibrium position.

Continuous Media and Sound Waves

A sound wave is simply an elastic wave travelling in a medium. For a material regarded as an elastic continuum, the sound velocity is then directly related to the elastic modulus of the material. The sound produces a spatially varying stress s which in turn causes an instantaneous displacement u. If the sound is propagating in the x direction within a cube of material of mass density r, the net force acting on the volume element is:

is a measure of the velocity of a wave packet, composed of a group of plane waves, and having a narrow spread of frequencies about some mean value, w. For acoustic waves with long wavelengths (k » 0), i.e. in the elastic continuum limit, the phase and group velocities are equal. In a liquid, only longitudinal vibrations (modes) are supported (shear modulus is zero). The situation is more complicated in solids , where more than one elastic modulus is non-zero. As a consequence, both longitudinal and transverse acoustic modes exist even in isotropic solids, having in general different sound velocities. The situation is even more complicated for anisotropic crystals.

Counting vibrational states

The wavevector k characterises the vibrational wave. In the general solution to the wave equation, Eqn. 5, all k values are allowed. Restrictions on the allowed values of k appear through the imposition of boundary conditions. Two types of boundary conditions can be envisaged, depending on whether standing waves or propagating waves are involved.
For standing waves, and considering a cube of material of side L, the appropriate boundary condition for vibrational waves reflected from mechanically free surfaces is that an antinode of the vibration amplitude should exist at each surface. This corresponds to there being an integral number of half-wavelengths of the standing wave along the length of the cube. The allowed values of the standing wave vectors are given by

Schematic 1D illustration of a standing wave set up between the free surfaces of a cube of an elastic continuum with antinodes at the free surfaces.
Each allowed standing-wave solution of the wave equation consistent with the boundary conditions is represented by a point in the reciprocal space containing the k-vectors. The spacing between allowed k-values is Dks=p/L, and so the volume of k-space corresponding to the one k-value (standing-wave state).

ORLANING COLMENARES

C.I.V.-18.991.089

Visitar mi BLOG:

http://orlaningcaf.blogspot.com

BIBLIOGRAFIA:

www.plato.ul.ie/academic/Vincent.Casey/PH4607SS1/LatticeDynamics.doc

---

Connect to the next generation of MSN Messenger  Get it now!