The presence of translational periodicity has a profound effect on the vibrational behaviour when the wavelength of the vibrational excitations becomes comparable to the periodic repeat distance, a. For l>>a, however, the behaviour characteristic of an elastic continuum is recovered.
For a periodic array of atoms of length L, periodic (or Born-von Karman) boundary conditions are appropriate, i.e.
Such a boundary condition can be envisged as follows. In the case of a linear chain of N particles, where the nearest neighbours are connected by springs (representing bonds between atoms), with equilibrium spacing a, periodic boundary conditions are achieved by connecting one end of the chain to the other to form a ring of length L=Na, Figure 4a. An integral number of wavelengths must fit into the length L, resulting in allowed K-values for running-wave (travelling wave) states:
An equivalent and more realistic way of understanding periodic boundary conditions involves the imposition of a mechanical constraint forcing atom N to interact with atom 1 via a massless, rigid rod and a spring, Figure 4b.
In contrast to the case for fixed boundary conditions leading to stationary waves, both positive and negative integers are allowed for running wave solutions, and moreover the spacing between allowed k-values is Dkr=2p/L, twice that for standing wave states. Therefore, the number of k-values, corresponding to running wave states, contained in unit volume of k-space is now
In contrast to the case for fixed boundary conditions leading to stationary waves, both positive and negative integers are allowed for running wave solutions, and moreover the spacing between allowed k-values is Dkr=2p/L, twice that for standing wave states. Therefore, the number of k-values, corresponding to running wave states, contained in unit volume of k-space is now
The number of distinct states, for a given polarisation type i, having wavevectors between k and k + dk is this density multiplied by the volume of an entire spherical shell in k-space (since both positive and negative k-values are allowed)
A linear chain connected to form a ring of length L=8a. For modes of the form us ~exp (iska), periodic boundary conditions lead to eight modes (one per atom) with k=0, ±2pi/L, ±4pi/L, ±6pi/L, ±8pi/L.· All atoms identical (mass m)
· Lattice spacing 'a'
For small vibrations, the force on any one atom is proportional to its displacement relative to all the other atoms.
Choose atom s
· p takes on both positive and negative values
· c is the force constant and depends on p, i.e. is large for p=1, smaller for p=2, etc..
· c is the force constant and depends on p, i.e. is large for p=1, smaller for p=2, etc..
The displacement for k' is therefore the same as for k. k' consists of a wave of smaller wavelength than that corresponding to k, passing through all the atoms, but containing more oscillations than needed for the description.
We can describe the displacement of the atoms in these vibrations most easily by looking at the limiting cases k = 0 and k = p/a.
· the situation at k = 0 corresponds to an infinite wavelength; this means that all of the atoms of the lattice are displaced in the same direction from their rest position by the same displacement magnitude. For long wavelength vibrations neighbouring atoms are displaced by the same amount in the same direction. Since the long-wavelength longitudinal vibrations correspond to sound waves in the crystal, all of these vibrations with a similarly shaped dispersion curve, whether transverse or longitudinal vibrations are involved, are called acoustical branches of the vibration spectrum. [When k @ 0, dw/dk = w/k = velocity of sound]
We can describe the displacement of the atoms in these vibrations most easily by looking at the limiting cases k = 0 and k = p/a.
· the situation at k = 0 corresponds to an infinite wavelength; this means that all of the atoms of the lattice are displaced in the same direction from their rest position by the same displacement magnitude. For long wavelength vibrations neighbouring atoms are displaced by the same amount in the same direction. Since the long-wavelength longitudinal vibrations correspond to sound waves in the crystal, all of these vibrations with a similarly shaped dispersion curve, whether transverse or longitudinal vibrations are involved, are called acoustical branches of the vibration spectrum. [When k @ 0, dw/dk = w/k = velocity of sound]
In addition to longitudinal vibrations, the linear lattice supports transverse displacements leading to two independent sets (in mutually perpendicular planes) of vibrations that can propagate along the lattice. The forces acting in a transverse displacement are weaker
than those in a longitudinal one. They give rise to a new branch of dispersive modes lying below the longitudinal branch.
ORLANING COLMENARES
C.I.V.- 18.991.089
REFERENCIAS BIBLIOGRAFICAS:
www.plato.ul.ie/academic/Vincent.Casey/PH4607SS1/LatticeDynamics.doc
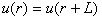







No hay comentarios:
Publicar un comentario